La constante de aparcamiento de Rényi trata de estimar el espacio que se utiliza realmente para aparcar en una línea recta. La cifra a la que llega, mediante estimaciones matemáticas bastante alejadas de la compleja realidad, es que se utiliza aproximadamente un 74,76% del espacio.
Es decir, en 100 metros de acera, tan sólo 74,76 metros estarían ocupados por coches, el resto sería espacio libre.
Su teoría es correcta para estimar, por ejemplo, cuantos caramelos de tamaño fijo podemos poner en un espacio colocándolos aleatoriamente hasta que no queden huecos vacios. Pero la realidad es que el aparcamiento no sigue esta regla, y a continuación os propongo unos factores de por qué ese número no tiene por qué ajustarse a la realidad:
-
Al contrario que los caramelos, los coches no miden lo mismo
-
Al contrario que los caramelos, los coches necesitan más espacio para aparcarse que su longitud. Si tu coche mide 4 metros, es imposible aparcarlo en un sitio con cuatro metros. Además, el espacio extra depende de la persona, ¡y del coche!, ya que no todos son igual de “fáciles” de aparcar.
-
La elección de sitio no es aleatoria. Algunos tratarán de elegir el sitio más pequeño en el que quepa su coche, y otros, más egoístas, el más grande.
-
Un segmento de acera no pasa de estar completamente libre a completamente ocupado, los coches van rotando.
Al igual que en informática (asignación de memoria a procesos), existe el problema de la fragmentacion interna y externa.
Fragmentación interna es que, si a 5 coches les sobran 1 metro a cada uno en su espacio, no podrá aparcar otro coche, a pesar de que hay “5 metros libres”. La externa es que, si hay 103 metros de acera y quieren aparcar 20 coches que utilicen exactamente 5 metros, se estarán desperdiciando 3 metros en los que no se puede meter nada.
Si ese coche hubiera aparcado mejor, yo podría meterlo ahí (I)
A menudo oigo esa frase cuando estoy con alguien buscando dónde aparcar. Cierto, al ver un coche en medio de un sitio en el que cabrían dos coches, la sensación de frustración suele aparecer. ¿Pero es necesariamente el conductor de ese coche un egoísta que aparca mal? La respuesta es no. Al menos, no lo podemos asegurar, con lo cual antes de acordarnos de su familia, deberemos tener en cuenta que puede que no haya hecho nada malo. ¿Y cómo es eso? Vamos a ver un ejemplo:
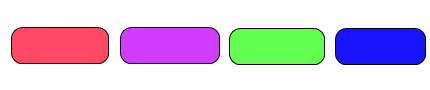

Figura 2: El coche representado por el rectángulo verde se va.

Figura 3: El coche naranja aparca. Es más pequeño, y decide pegarse al de delante (también podría haber decidido pegarse al de atrás). En cualquier caso, actúa correctamente.

Figura 4: El coche rosa se va.

Figura 5: Llega otro coche (verde), y se pega a la izquierda, también esta actuando correctamente. Si alguien pasa por allí verá que hay espacio para un quinto coche, si el violeta estuviese más adelante o más atrás el quinto coche podría aparcar. Sin embargo, el coche violeta aparcó bien cuando llegó, y el resto también, y aún así se produce este problema (fragmentación externa).
Con este ejemplo vemos que el aparcamiento es “inherentemente caótico”, y que no siempre estas situaciones se producen porque la gente haga las cosas mal. Dicho esto, tengo que opinar que una grandísima mayoría de los conductores aparca mal, ayudando así a este caos.
Si ese coche hubiera aparcado mejor, yo podría meterlo ahí (II)
Si ese coche hubiera aparcado mejor, otro hubiera cogido el sitio. Porque es posible que lleve así 10 horas y hayan pasado mil coches buscando donde aparcar. Si el gordo de navidad cae en 23.402 y tú tienes el 23.403, no es que no hayas ganado por poco, has perdido igual que el que tiene el 00000. (No es un buen ejemplo porque en la lotería el número siguiente al gordo tiene premio, pero nos sirve para ilustrar el pensamiento erróneo respecto a la probabilidad de tener éxito).
Como véis, el tema da para escribir un libro (o una enciclopedia). El caso es que no es algo controlable como conductores, así que lo mejor es relajarse y buscar sitio hasta encontrar uno libre. Desgraciadamente, aún después del relajante momento de haber aparcado, todavía hay más peligros.
Vía | Microsiervos
Más información | Rényi’s Parking Constants
En Motorpasión | Historias de aparcamientos, con video ilustrativo
�




Ver 25 comentarios